
Családi ház gázfogyasztása

| fűtési évad | állapot | gázfogyasztás
(m3)
mint a napi átlaghőmérséklet (oC) függvénye |
gázfogyasztás
0 oC
napi átlaghőmérsékletnél |
csökkentés |
| 2004/2005 | eredeti állapot | V=17,49-1,045 T | 17,49 | 100 % |
| 2005/2006 | ablakok és ajtók höszigetelése | V= 14,11-0,839 T | 14,11 | 81 % |
| 2006/2007 | + Drywit hőszigetelés (8 cm) | V= 9,20-0,592 T | 9,20 | 53 % |
| 2007/2008 | + C-24 cirko helyett INKA 24V kondenzációs cirko + villanybojler helyett gázbojler |
V= 9,84-0,661 T | 9,84 | 56 % |
| 2008/2009 | javitott cirko hőmérséklet-programozás: | V= 9,36-0,637 T | 9,36 | 54% |
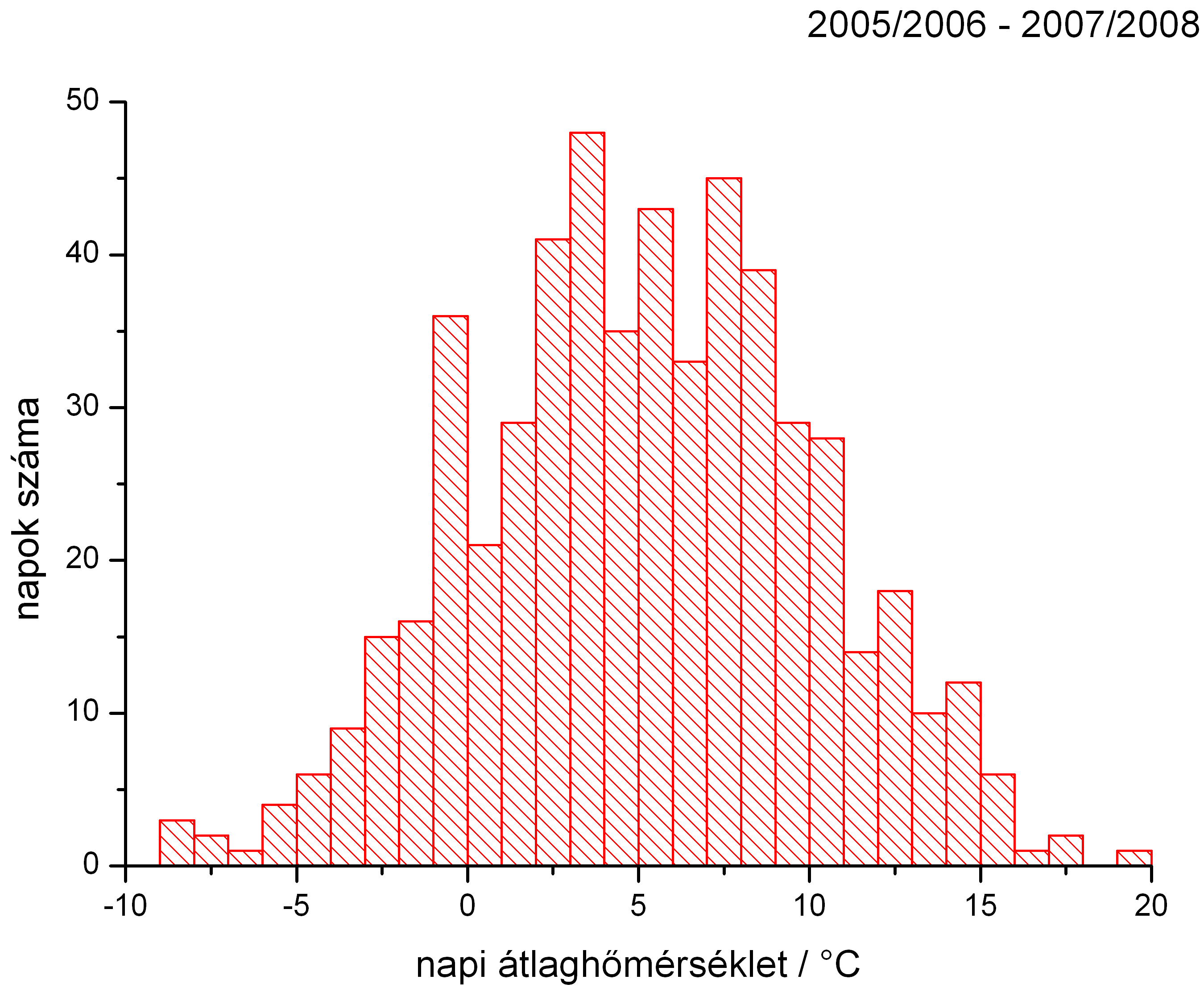
Az egyes napi átlaghőmérsékletek gyakorisága a 2005/06, 2006/07 és 2007/08 fűtési idényekben együtt. Látható, hogy a -5 oC-nál alacsonyabb napi átlaghőmérséklet nagyon ritka Budapesten.
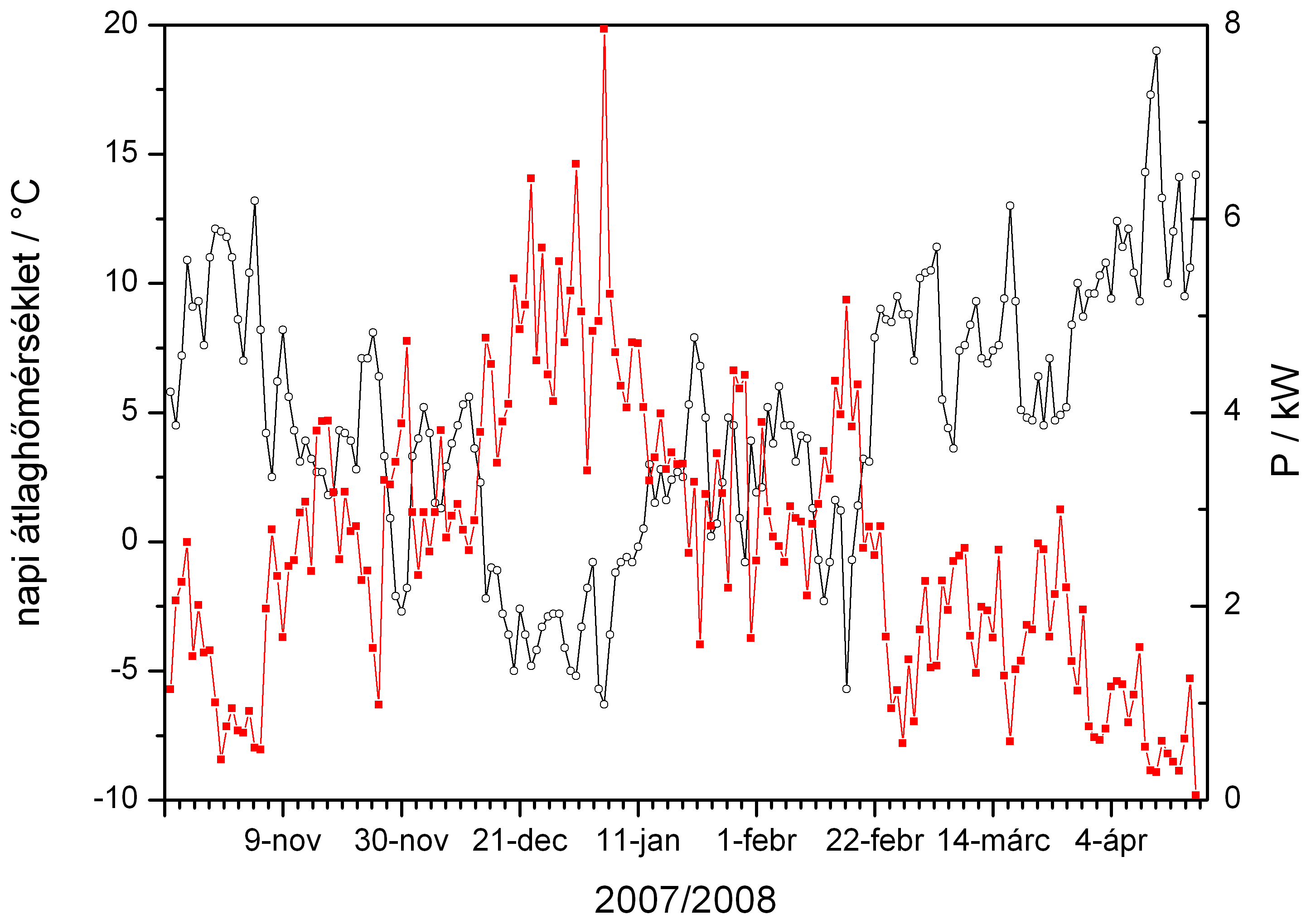
A 2007/2008 fűtési idényben az egyes napokon az átlaghőmérséklet és a napi átlagos kazánteljesítmény. A napi átlagos kazánteljesítményt a földgáz-fogyasztásból számítottuk. Ha folyamatosan üzemelt volna a cirkó, három nap kivételével soha nem lett volna szükség 6 kW-nál nagyobb fűtési teljesítményre. A cirkó 24 kW teljesítményű.
Miért
energiatakarékosabb a kondenzációs cirkó, mint a hagyományos?
Az alábbi ábra megmutatja egy kondenzációs kazán számított hatásfokának változását a visszatérő melegvíz hőmérsékletének függvényében, összehasonlítva azt egy olyan hagyományos cirkó hatásfokával (ezt vesszük 100%-nak), amelynél a füstgáz 150 °C hőmérsékleten távozik a kéményen keresztül.
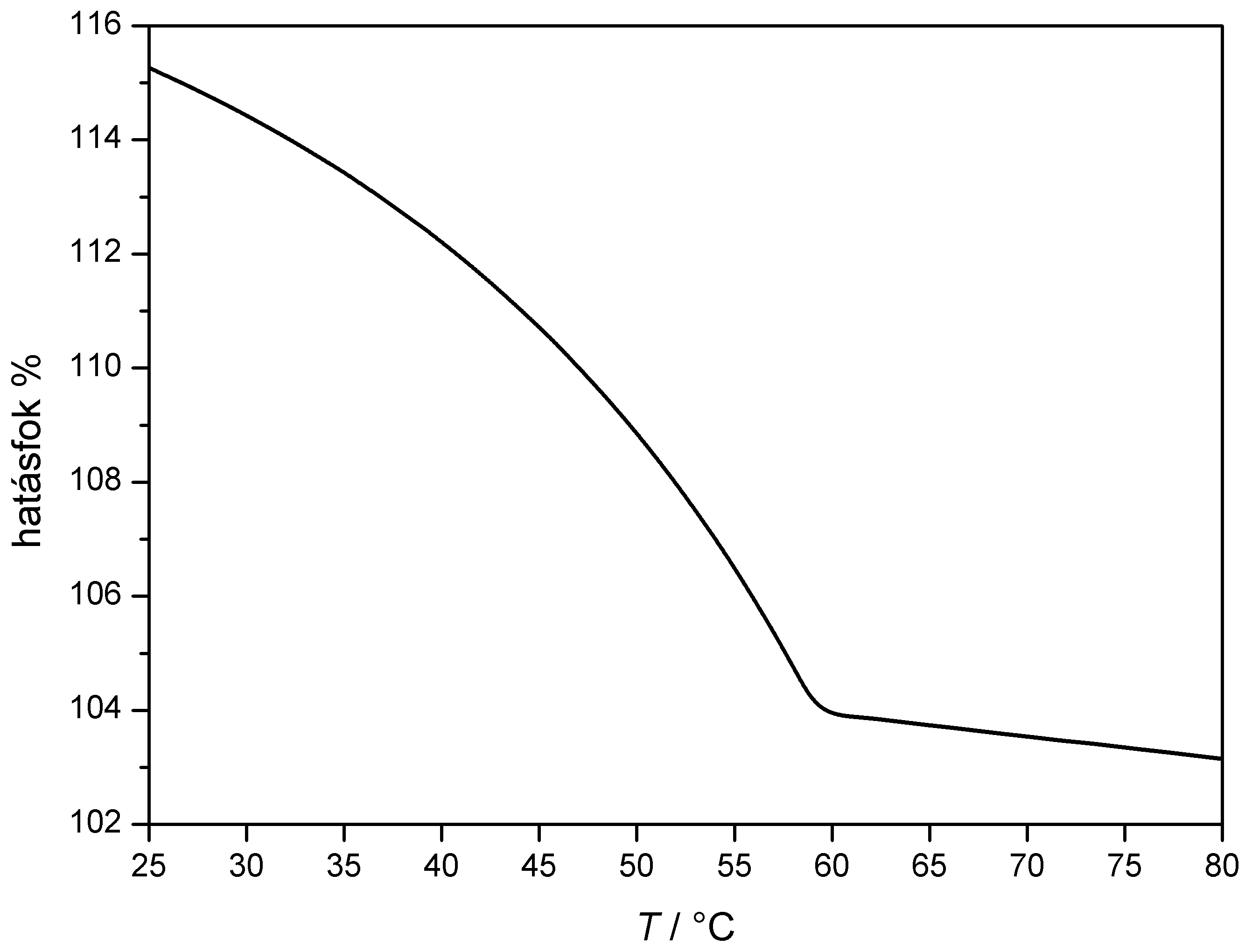
A
hagyományos
cirkóval szemben elsősorban azért magasabb egy
kondenzációs kazán hatásfoka,
mert hasznosítja a víz kondenzációs
hőjét, illetve mert a füstgáz alacsonyabb
hőfokon távozik. Ennek megfelelően a hőcserélő
hőmérsékletét növelve a
kondenzáció arányának
csökkenésével erősen romlik a hatásfok, majd
a
kondenzáció megszünte után a hatásfok
kissé tovább csökken, mert a kiáramló
füstgáz hőmérséklete növekszik.
A fenti ábrákat kizárólag középiskolai kémia és fizika ismeretek alapján meg lehetett szerkeszteni. Akinek van türelme, olvassa el az alábbi középiskolai kémiapéldát. (Megjelent a Középiskolai Kémiai Lapok 2008/4. számában, H95 példa.)
a)
A háztartási
gázórán leolvasott gázfogyasztás
úgynevezett gáztechnikai normálállapotra
vonatkozik (1 atm nyomás és 15 °C hőmérséklet).
Mennyi hő szabadul fel 1 m3 térfogatú,
gáztechnikai normálállapotú
metán égésekor, ha a keletkező víz légnemű és mennyi, ha a keletkező
víz
folyékony? Csak ezt a hatást tekintve, mennyivel lehet nagyobb egy
kondenzációs
kazán hatásfoka?
b)
Egy hagyományos
cirkó fali gázkazánnál a 150 °C
hőmérsékletű
füstgáz a kéményen át távozott.
A kondenzációs cirkónkból az 50 °C
hőmérsékletű füstgázt egy
ventilátor hajtja ki. Mi a füstgáz
összetétele (mol%) a kétféle cirkó
esetén?
Mennyi hő fűti a házat a kétféle cirkó
esetén, ha a gázóra szerint 1,000 m3
földgáz fogyott?
Tételezzük fel, hogy a földgáz csak metánból áll, a levegő összetétele 21 mol% O2 és 79 mol% N2, valamint hogy az égés mindkét esetben sztöchiometrikus, tehát a füstgázban nem marad sem metán, sem oxigén. A cirkó gázégőjében az égés előtt a földgáz és a levegő is 25 °C hőmérsékletű és 1 bar nyomású.
A szükséges adatok, mind 25 °C hőmérsékleten és 1 bar nyomáson: a képződési entalpiák: DHfo(CH4) = -74,81 kJ mol-1, DHfo(CO2) = -393,51 kJ mol-1, DHfo(H2O(g)) = -241,82 kJ mol-1, DHfo(H2O(l) = -285,83 kJ mol-1. A résztvevő anyagok állandó nyomáson vett moláris hőkapacitása: Cp(CO2)= 37,11 J K-1 mol-1, Cp(H2O(g))= 33,58 J K-1 mol-1, Cp(H2O(l))= 75,291 J K-1 mol-1, Cp(N2)= 29,125 J K-1 mol-1. A víz egyensúlyi gőznyomása 12332 Pa 50 °C hőmérsékleten.
Megoldás:
a)
A
reakcióegyenlet:
CH4 + 2 O2
= CO2 + 2 H2O
A standard
moláris
reakcióentalpia 25 °C hőmérsékleten,
ha
vízgőz keletkezik:
DrHo = –1 × DHfo(CH4)
– 2 × DHfo(O2)
+1 × DHfo(CO2)
+ 2 × DHfo(H2O(g))
DrHo = (–1 × –74,81 –2 × 0 + 1 × –393,51 + 2 × –241,82) kJ mol-1=
–802,34 kJ mol-1
A standard
moláris
reakcióentalpia 25 °C hőmérsékleten,
ha
folyékony víz keletkezik:
DrHo = –1 × DHfo(CH4)
– 2 × DHfo(O2)
+1 × DHfo(CO2)
+ 2 × DHfo(H2O(l))
DrHo = (–1 × –74,81 –2 × 0 + 1 × –393,51 + 2 × –285,83) kJ mol-1
= –890,36 kJ mol-1
pV=nRT
n=pV/RT = (101325
Pa × 1 m3)/
(8,314 J
K-1 mol-1 × 288,15 K) =
42,295
mol
Ha a metánt
tökéletes gáznak tekintjük, a fenti körülmények között 1 m3
tehát
42,295
mol metánt tartalmaz.
Ha H2O(g)
keletkezik, akkor 1 m3 metán elégésekor q=
42,295 mol × –802,34 kJ mol-1
= –33935 kJ = –33,935 MJ a hőváltozás. (A gázművek 34 MJ/m3 fűtőértékkel
számol.)
Ha H2O(l)
keletkezik, akkor 1 m3 metán elégésekor q=
42,295 mol × –890,36 kJ mol-1
=
Ez utóbbi 10,97
%-al
több, tehát ennyivel lenne nagyobb egy kondenzációs kazán hatásfoka, ha
minden
vízgőz kondenzál és a reakciótermékek 25 °C hőmérsékletűek.
b.)
Hagyományos
cirkó: A levegőben 0,21 mol O2-re
0,79 mol N2 jut, tehát 1 mol O2-re
0,79/0,21=3,7619 mol N2,
illetve 2 mol O2-re 2 × 3,7619= 7,5238
mol N2
jut. Az égés egyenlete CH4 + 2 O2
= CO2 + 2 H2O,
tehát sztöchiometrikus égés esetén 1 mol CH4
elégésekor a
hagyományos cirkó füstgáza 1,0000 mol CO2-t,
2,0000 mol H2O-t
és 7,5238 mol N2-t tartalmaz (összesen 10,5238
mol).
A füstgáz
összetétele tehát
x(CO2)=1/10,5238 × 100= 9,502%,
x(H2O)=2/10,5238 × 100= 19,005%,
x(N2)=
7,5238/10,5238 × 100= 71,493%
A füstgázelegy
moláris hőkapacitása:
Cp = x(CO2) × Cpm(CO2)
+ x(H2O) × Cpm(H2O)
+ x(N2) × Cpm(N2)=
(0,09502 × 37,11 + 0,19005 × 33,58 + 0,71493 × 29,125) J K-1
mol-1
= 30,7304 J K-1 mol-1
1 mol ilyen
gázelegy
felmelegítéséhez szükséges hő 25 °C-ról
150 °C-ra:
DH = 1
mol × +30,7304 J K-1
mol-1 × 125 K = +3841,30 J
1 mol CH4
elégésekor 10,5238 mol füstgáz keletkezik, ekkor 10,5238 × 3841,30 J =
+40425
J = +40,425 kJ kell a füstgáz
felmelegítésére, tehát 1 mol
földgáz elégetésekor hasznosul –802,34
kJ × + 40,41
kJ mol-1 = –761,93 kJ hő. A tökéletes gázok
törvénye alapján 1 m3
térfogatú, 1 atm nyomású és 15 °C hőmérsékletű
metán 42,295 mol,
tehát 1 m3
földgáz égéséből 42,295
mol × –761,93 kJ =
–32226 kJ = –32,226
MJ hő hasznosítható. A hatásfok
a gáz fűtőértékéhez képest –761,93/–802,34 = 95,0 %.
Kondenzációs
cirkó
esetén az alacsony
füstgáz-hőmérséklet miatt a keletkező
víz egy része lecsapódik és a
füstgáz
telített lesz vízgőzre. A víz egyensúlyi
gőznyomása ezen a hőmérsékleten 12332
Pa, tehát a víz aránya a füstgázban
x(H2O)=12332
Pa / 100000 Pa = 12,332 mol%.
A maradék
(100,000 –
12,332) mol% = 87,668 mol% a CO2 és az N2
között 1 :
7,5238 arányban oszlik meg, tehát
x(CO2)=
1/8,5238 × 87,668 mol%=
10,285
mol%,
x(N2)=
7,5238/8,5238 × 87,668 mol%=
77,383
mol%.
Ez azt is
jelenti,
hogy minden 1 mol keletkező CO2 mellett
12,332/10,285=1,1990 mol víz
lesz légnemű és 2,000–1,199=0,801 mol vízből lesz folyadék.
Elhanyagoltuk, hogy
a CO2 egy része a lecsapódó vízben feloldódik. A
CO2 oldódása
nem változtatja meg a lecsapódó víz
arányát, de csökkenti a füstgázban
a CO2 koncentrációját.
A kondenzációs
cirkó esetén az adott körülményeknél a termokémiai
egyenlet, figyelembe véve, hogy a fenti arányban keletkezik légnemű és
folyékony víz:
CH4(g)
+
2 O2(g) = CO2(g) + 1,199 H2O(g)
+ 0,801 H2O(l)
A megfelelő
moláris
entalpiaváltozás:
DrHo= –1 × DHfo(CH4)
– 2 × DHfo(O2)
+1 × DHfo(CO2)
+ 1,199 × DHfo(H2O(g))
+ 0,801 × DHfo(H2O(l))
DrHo = –1 × –74,81 –2 × 0 +1 × –393,51 +1,199 × –241,82+0,801 × –285,83=
–837,5920 kJ mol-1
Ilyenkor a
füstgáz-elegy moláris hőkapacitása:
Cp = (37,11 × 0,10285 + 33,58 × 0,12332 + 29,125 × 0,77383) J mol-1
= 30,496 J mol-1
1 mol CH4
elégésekor (1,0000+7,5238+1,1990) mol = 9,7228 mol füstgáz
keletkezik, és
ennek a 25 °C-ról
50 °C-ra
felmelegítéséhez
szükséges entalpia:
DH = 9,7228 mol × +30,49 J K-1
mol-1
× 25 K = +7411,2 J = +7,4112
kJ
A folyékony víz
moláris hőkapacitása 75,291 J K-1 mol-1,
tehát a
keletkező 0,801 mol folyékony víz felmelegítéséhez szükséges
hőmennyiség:
DH = 0,801 mol × +75,291 J K-1
mol-1 × 25 K = +1507,7 J =
+1,5077 kJ.
Egy mol földgáz
elégetésekor hasznosul –837,5920 kJ + 7,4112 kJ +1,5077 kJ = –828,6731 kJ. A tökéletes gázok
törvénye
alapján 1 m3 térfogatú, 1 atm nyomású és 15 °C hőmérsékletű
metán 42,295 mol,
tehát 1 m3 földgáz
égéséből 42,295 mol
× –828,6731 kJ =
–35049 kJ =
–35,049 MJ
hasznosítható. A hatásfok a gáz
fűtőértékéhez képest
–828,67/–802,34 = 103,3 %.
Egy m3földgáz
égésekor tehát 32,226 MJ hőt hasznosítunk a
hagyományos és 35,049 MJ
hőt a kondenzációs cirkóban. A
kondenzációs cirkó tehát a
példában megadott
körülmények között 8,8 %-al jobban
hasznosítja a földgáz égéséből
származó hőt.
Végezzük el a fenti számítást minden
egész füstgáz hőmérsékletértékre 25 °C és 80 °C között! A
számításokhoz ismernünk kell a víz
egyensúlyi gőznyomásának
hőmérsékletfüggését,
aminek táblázatát könyvtárban
(Handbook of Chemistry and Physics: 73rd
Edition (1992-93)) vagy az Internetről
(http://dbhs.wvusd.k12.ca.us/webdocs/GasLaw/Vapor-Pressure-Data.html)
szerezhetjük be. A számításokat táblázatkezelővel (Excel) elvégezve azt
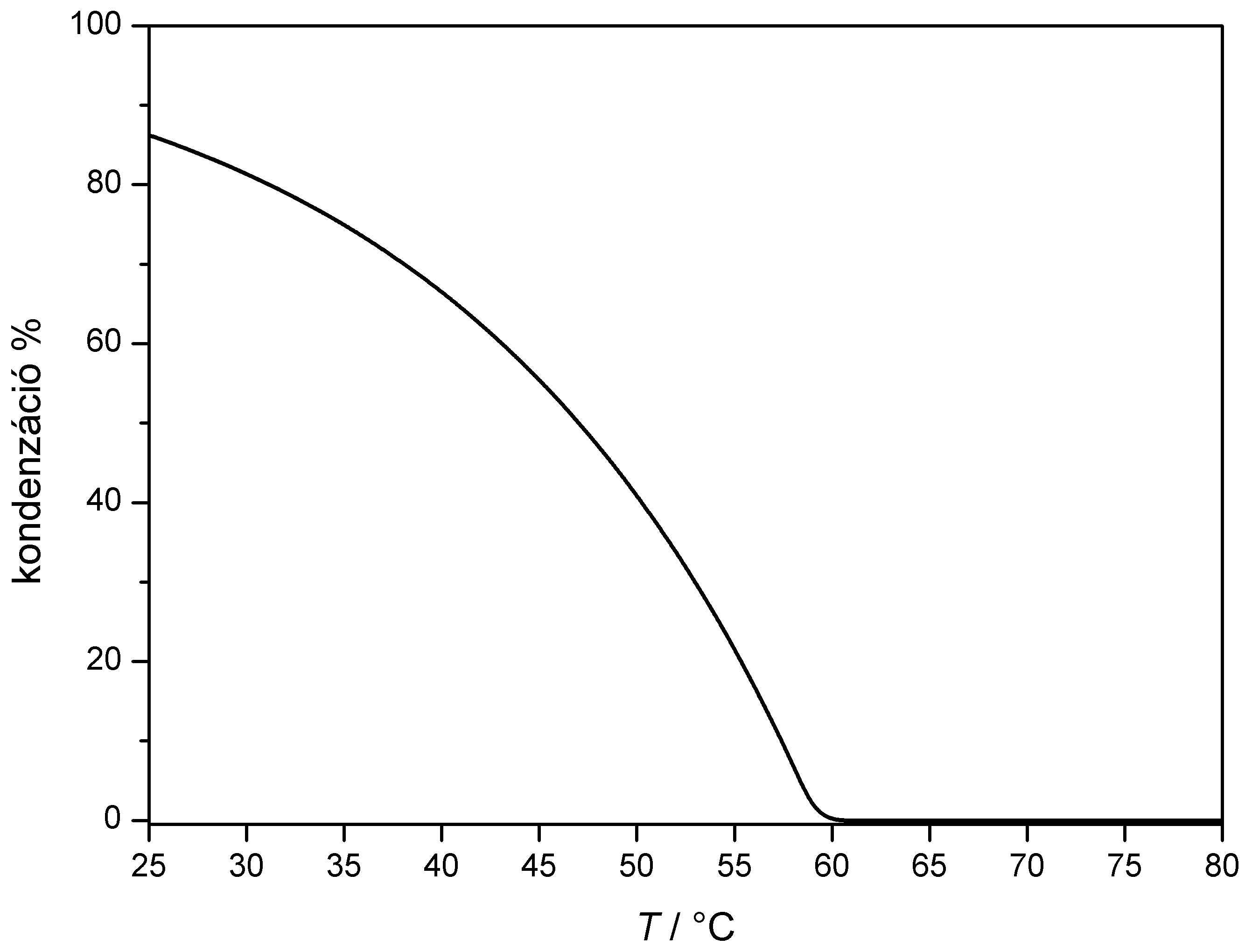
láthatjuk, hogy az égés során keletkező víznek közel 80%-a kondenzál 30
°C-on és 60 °C
felett egyáltalán
nincs kondenzáció. A fenti leírásból
látható, hogy a kondenzáció
mértéke a légnyomástól is függ!
Az
Excellel számított függvényeket
ábrázolva megkapjuk az oldal tetején
látható ábrákat.
Kérem írja meg megjegyzéseit Turányi Tamásnak
Utolsó módosítás: